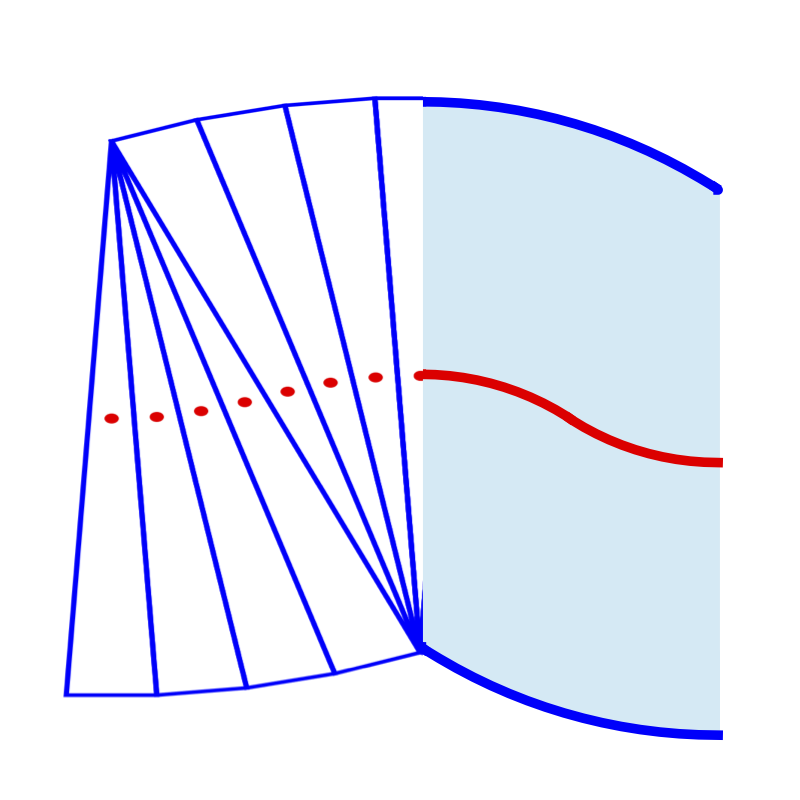
„Unbuckling“ eines minimalen Gewebemodells: Die Höhe der geknickten Form kann mit zunehmendem Druck abnehmen. © Chandraniva Guha Ray and Pierre A. Haas / MPI-CBG / MPIPKS
Viele der faltigen Formen, die während der Entwicklung auftreten, zum Beispiel im Gehirn und im Darm, sind auf mechanische Instabilitäten zurückzuführen. Diese Faltung von Zellschichten ist entscheidend für die Funktion von Gewebe und Organen.
Chandraniva Guha Ray und Pierre Haas vom Max-Planck-Institut für molekulare Zellbiologie und Genetik (MPI-CBG), vom Max-Planck-Institut für Physik komplexer Systeme (MPIPKS), und vom Zentrum für Systembiologie Dresden (CSBD) haben nun gezeigt, dass sich diese mechanischen Instabilitäten von Geweben stark von den klassischen Instabilitäten wie der Faltung von Papier unter Druck unterscheiden können. Je stärker ein Blatt Papier zusammengedrückt wird, desto mehr nimmt auch die Höhe der geknickten Form zu. Chandraniva Guha Ray, Doktorand in der Forschungsgruppe von Pierre Haas, erklärt, warum dies nicht der Fall ist bei einem einfachen theoretischen Gewebe-Modell, das aus einzelnen Zellen besteht: „Wenn sich ein Gewebe faltet, biegen sich die Zellseiten, was dazu führt, dass die Ober- oder Unterseite der Zelle schrumpft, bis diese sich nicht mehr biegen können. Diese unerwartete Folge, die wir ‚unbuckling‘ nennen: mit zunehmendem Druck, kann die Höhe der geknickten Form abnehmen.“
Pierre Haas, Forschungsgruppenleiter am MPI-CBG, am MPIPKS, und am CSBD, fasst zusammen: „Unsere Berechnungen zeigen, dass dieses ‚unbuckling‘ die Festigkeit des Gewebes enorm erhöht.“ Zu den Gewebefalten, die auf diesem Mechanismus beruhen könnten, gehört beispielsweise die Kopffalte der Fruchtfliege Drosophila, die kürzlich von der Gruppe von Pavel Tomancak am MPI-CBG untersucht wurde. Pierre ergänzt: „Diese minimalen mechanischen Modelle sind nützlich, weil sie es uns ermöglichen, mechanische Instabilitäten im Detail zu verstehen und damit auch, wie die Zellmechanik zu biologischer Form und Funktion auf der Ebene der Gewebe führt.“
Chandraniva Guha Ray and Pierre A. Haas, Phys. Rev. Lett. 134, 118402 (2025). https://doi.org/10.1103/PhysRevLett.134.118402