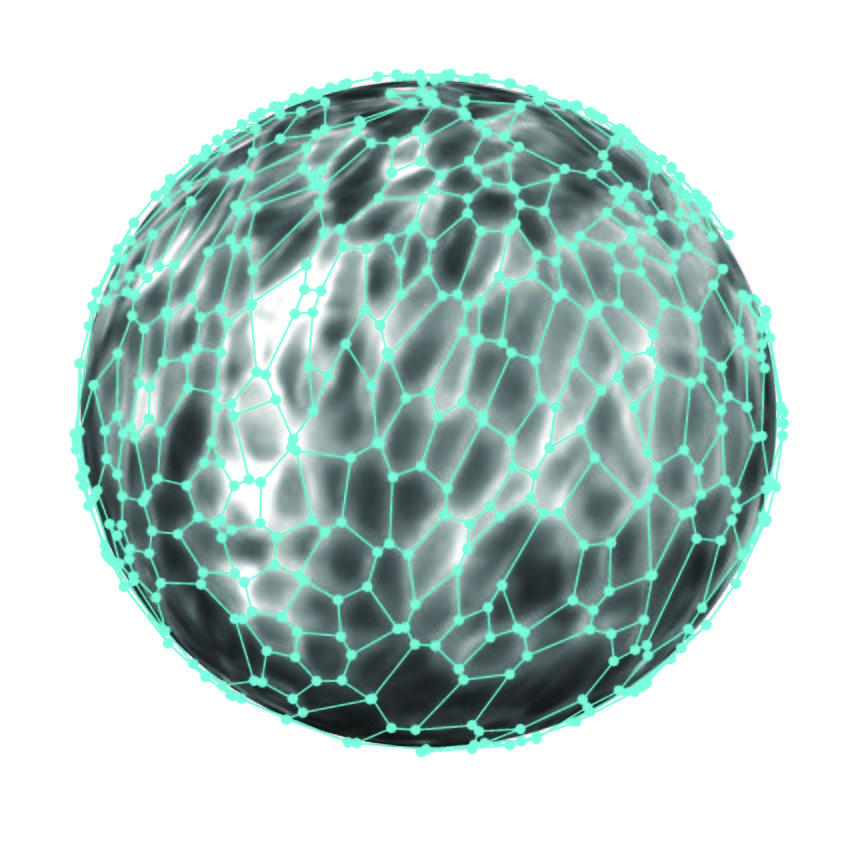
Cell segmentation (cyan) performed on the projection of a pancreas sphere. © Tzer Han Tan et al. PRX Life 2024 / MPI-CBG
Collective cell dynamics, when groups of cells move together, are crucial in many biological systems. The way these cells move, align with each other, and interact mechanically creates new patterns and behaviors that are essential for their function. While much is known about how cells migrate in two dimensions (2D), the effects of three-dimensional (3D) environments on collective cell behavior are less understood.
The research groups of Anne Grapin-Botton at the Max Planck Institute of Molecular Cell Biology and Genetics and of Frank Jülicher and Marko Popović, both at the Max Planck Institute for the Physics of Complex Systems, set out to investigate the rotation of spherical cell clusters. The researchers looked at lab-grown mouse pancreas organoids—models of an organ in three dimensions. Tissue rotation is quite common and is also observed in other organoid systems or in embryos.
“We found that many of these cell clusters rotate continuously, with the direction of rotation sometimes drifting or stopping entirely,” says Tzer Han Tan, one of the three lead authors of the study. He continues, “We asked ourselves why the cell clusters (or organoids) are rotating and reached out to our physicist colleagues Frank Jülicher and Marko Popović.” The researchers built a three-dimensional physical model to understand the collective cell behavior. Those 3D vertex models are usually used to describe other things, but here, the researchers added a polarity vector for cells to the system and set up the model on a round sphere. “By running a simulation and then comparing it with experimental data for rotation speed and the stability of the rotation axis, we were able to show that the interplay of traction forces and cell polarity can explain these rotational behaviors,” say Frank Jülicher and Marko Popović.
Spherical tissue rotates solidly most of the time, like the earth, but the sphere can sometimes transition to a flowing state and spontaneously break symmetry. The collective cell behavior can give rise to this chiral asymmetry in three dimensions. An object or a system can be described as chiral if it is distinguishable from its mirror image. Both rotational motion and turbulent flows are necessary to achieve chiral asymmetry.
Anne Grapin-Botton, one of the three supervising authors, summarizes, “The robust mechanism for chiral symmetry breaking that we have discovered may have implications to understand the development of left-right asymmetry in biological systems. Our results most likely apply to rotating spheres composed of many cell types and in the pancreas may be deployed on other geometries such as tubes. This may be essential for understanding how cells behave on complex three-dimensional surfaces.”
Tzer Han Tan, Aboutaleb Amiri, Irene Seijo-Barandiaran, Michael F. Staddon, Anne Materne, Sandra Tomas, Charlie Duclut, Marko Popović, Anne Grapin-Botton, and Frank Jülicher: Emergent chirality in active solid rotation of pancreas spheres, PRX Life 2, 033006
https://doi.org/10.1103/PRXLife.2.033006